前缀和与差分是算法中常用的技巧，主要用于快速处理与区间操作相关的问题。它们各有适用的场景：

前缀和

用途：前缀和用于高效地求解数组中任意区间的元素之和。其思想是预先计算数组的累积和，从而在$O(1)$时间内求出任意区间的和。

解决的问题：

• 区间和查询：给定一个数组和多个区间，快速求解每个区间的和。
• 动态求和问题：通过提前构建前缀和数组，可以避免重复计算，提高效率。

更具体的问题:

对于一个数组$A = [1,5,8,6,2,4,9,7,3]$，它的区间是$[1,9]$这意味着第一个数的下标从1开始)，求区间$[3,6]$的和。

求$\sum_{i=3}^{6}A_{i}$，可表示为求

$$\sum_{i=1}^{6}A_{i} - \sum_{i=1}^{2}A_{i},$$

因为区间是双闭的，我们要确保$A_3$不被减去。因此我们定义一个前缀和数组$Sum$，令

$$Sum[i] = A_1 + A_2 + ... + A_i,$$

而对于$Sum$中除第一个元素外的所有元素，它们均可表示成

$$Sum[i] = Sum[i-1] + A_i(i >= 1),$$

这样，通过遍历一次数组$A$，我们就可以得到前缀和数组$Sum$:

观察数组$Sum$，如果我想知道区间$[3,6]$的和，那么我只需要知道$Sum[6] - Sum[2]$是多少就可以了。

A = [1, 5, 8, 6, 2, 4, 9, 7, 3]
Sum = [0]  # 将0写入Sum的第一个元素
# 防止i = 0时访问Sum数组数组越界
for i in range(len(A)):
    Sum.append(Sum[-1] + A[i])

print(f"数组A的区间[3,6]求和为:{Sum[6] - Sum[2]}")

细节处理：将$0$写入$Sum$的第一个元素后，我们会发现$Sum$数组比$A$数组多了一个元素，这会导致一个问题产生：当$i,j$均从下标1开始计算时，$Sum[j] - Sum[i-1]$求的是$[i,j]$的和，如果$i,j$从下标$0$开始，那么计算$Sum[j] - Sum[i-1]$求的就是$[i-1,j-1]$的和。

输出:

数组A的区间[3,6]求和为:20

推广：对于一个数组$a = [a_1, a_2, ..., a_n]$，定义前缀和数组$Sum$使得

$$Sum[i] = a_1 + a_2 + ... + a_i.$$

求区间$[i, j]$的和时，结果可以通过$Sum[j] - Sum[i-1]$快速得到。

差分

用途：差分用于高效地进行数组的区间更新操作。通过维护差分数组，可以在$O(1)$时间内对数组进行区间加减操作。

解决的问题：

• 区间增量更新：快速对一个数组的某个区间内所有元素进行相同的增量或减量操作。
• 批量更新问题：在需要对数组的多个区间进行批量操作时，差分方法可以显著降低复杂度。

更具体的问题:

对于相同的数组$A = [1,5,8,6,2,4,9,7,3]$，它的区间是$[1,9]$这意味着第一个数的下标从1开始)，现在对数组的$[1,3],[2,7],[2,5]$三个区间分别进行$+1,-2,+5$的操作，求进行加减操作后的数组$A$。

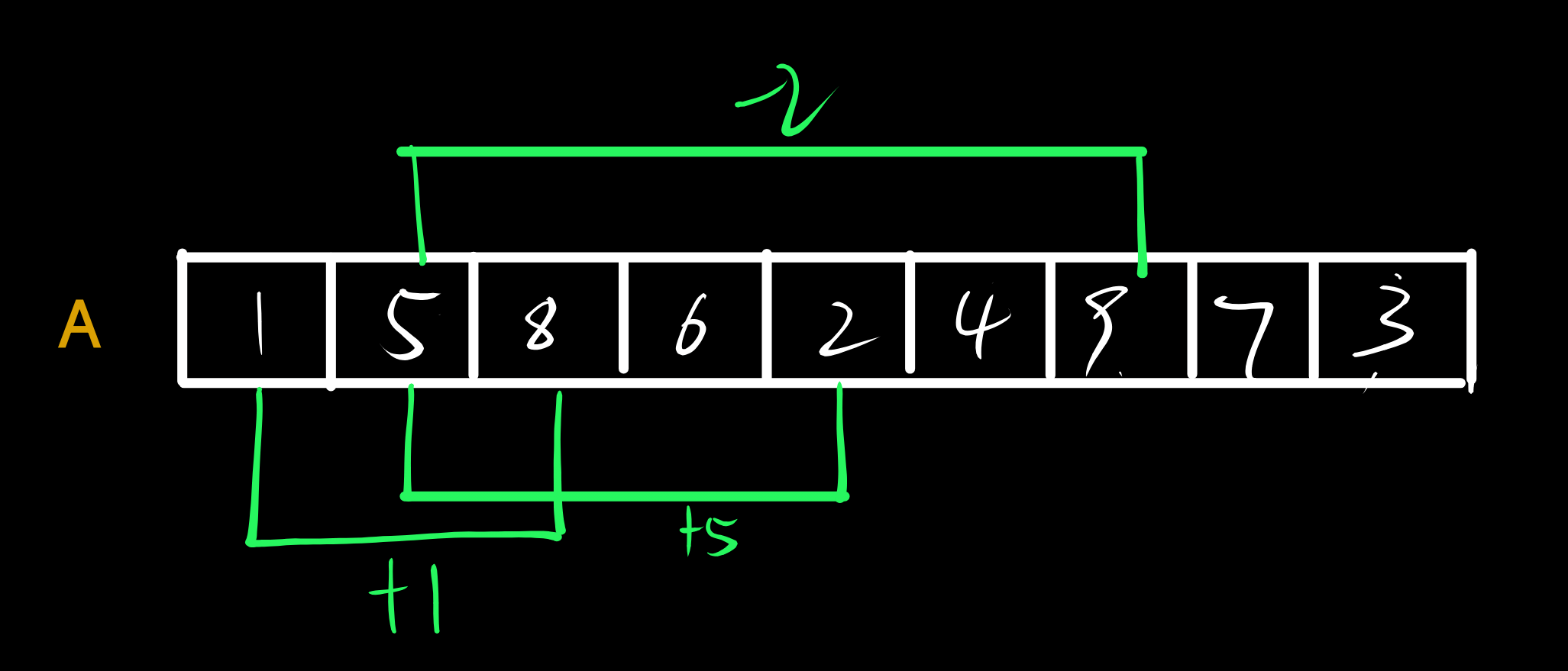
对数组$A$进行加减操作，常规的方式是对每一个区间进行遍历，对区间内的每一个元素作相应的处理，然而这种方式的效率很低，有没有一种方式可以实现对每一个区间进行加减操作时，只做常数级的运算呢？

通过构建数组

$$D[i] = A[i] - A[i-1](i > 0),$$

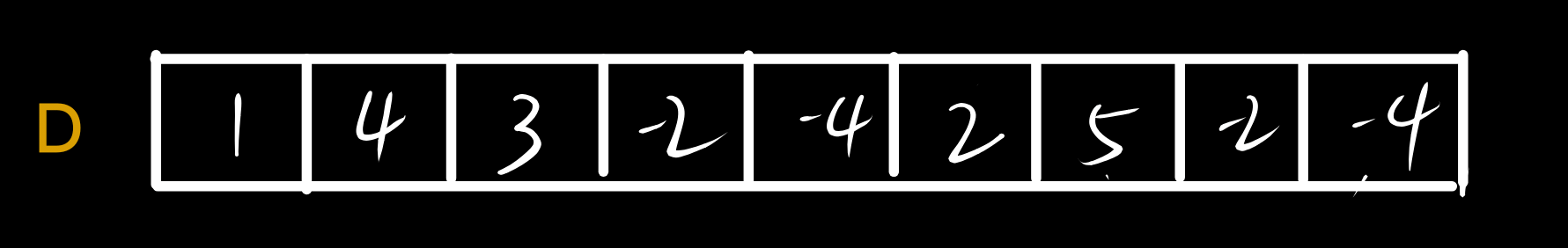
观察数组$D,D[i]$的含义是$A[i]$与$A[i-1]$的差值。在对区间$[i,j]$进行加减操作时，事实上区间$[i+1,j]$内的任意一个元素与它之前的一个元素之间的差值不会发生改变，只有第$i$个元素与第$i-1$(如果存在)个元素之间的差值和第$j+1$个元素与第$j$(如果存在)元素之间的差值(即为该区间每个元素的增减值)会发生变化。也就是说在数组$D$中，我们只需要修改$D[i]$和$D[j+1]$的值，即可更新数组的一次区间修改操作。

但是我们更新的一直都是数组$D$，我们需要的一直都是数组$A$。由数组$D$如何反推数组$A$呢？

由

$$D[i] = A[i] - A[i-1](i > 0),$$

则有

$$A[i] = D[i] + A[i-1](i > 0),A[0] = D[0],$$

我们会发现实际上这个过程就是对差分数组$D$进行一次前缀和的过程。

A = [1, 5, 8, 6, 2, 4, 9, 7, 3]
D = [0] # 将0写入D的第一个元素
        # 防止i = 0时访问D数组数组越界
for i in range(len(A)):
    D.append(A[i] - A[i-1])

op = [[1, 3, 1],[2, 7, -2],[2, 5, 5]]

for _ in op:
    D[_[0]] += _[2]
    D[_[1]+1] -= _[2]

for i in range(len(A)):
    A[i] = D[i+1] + A[i-1] # 访问差分数组时向后移一位
print(A)

细节处理：与前缀和类似，将$0$写入$D$的第一个元素后，我们会发现$D$数组比$A$数组多了一个元素，这会导致类似的问题产生，同时在对差分数组进行前缀和操作时，需要将差分数组向后移一位。

输出:

修改后的A数组为:[2, 9, 12, 9, 5, 2, 7, 7, 3]

推广：对于一个初始数组$a$，构建差分数组$D$使得$D[i] = a[i] - a[i-1]$（假设$a[0] = 0$）。要对区间$[l, r]$增加一个值$x$，只需执行D[l] += x和D[r+1] -= x。最终的数组可以通过累加差分数组得到。

两种算法的复杂度分析

方法	单次区间和查询	单次区间更新	预处理时间	空间复杂度
常规方法	$O(n)$	$O(n)$	$O(1)$	$O(1)$
前缀和	$O(1)$	$O(n)$	$O(n)$	$O(n)$
差分	$O(n)$ (还原)	$O(1)$	$O(n)$	$O(n)$

• 单次区间和查询：前缀和最优，能在 $O(1)$ 时间内完成；常规方法需要遍历区间，时间复杂度为 $O(n)$。
• 单次区间更新：差分算法最优，能够在 $O(1)$ 时间内完成；常规方法和前缀和方法则需要 $O(n)$ 时间。
• 预处理时间：两种算法都需要一次遍历来构建初始数据结构，时间复杂度为 $O(n)$。
• 空间复杂度：两种算法都需要额外的 $O(n)$ 空间来存储辅助数组。

优缺点总结:

• 前缀和：适用于频繁的区间和查询，查询效率高；但是在涉及频繁更新时，单次更新需要遍历，效率较低。
• 差分：适合频繁的区间更新，可以在 $O(1)$ 时间内处理；但查询区间和时需要恢复原数组，查询效率为 $O(n)$。
• 常规方法：不需要额外的存储，但对于大量查询或更新的场景，效率低。

典型应用

• 前缀和：用于解决问题如“求子数组和”以及“频繁查询区间和”的问题。
• 差分：适用于“区间加减操作”，如“批量增加区间内元素的值”或“更新二维平面上的值”。

两者都用于优化涉及频繁操作的算法，使之在时间复杂度上更高效。

再探索：增加一个维度

在实际应用中，数据不仅限于一维数组。二维数据（如矩阵或图像）在算法和数据处理中的应用也非常广泛。为了快速进行区间查询和更新操作，前缀和与差分这两种技巧可以扩展到二维，从而处理二维数据的区间问题。接下来，我们将详细讲解如何在二维空间中构建和使用前缀和与差分。

1. 二维前缀和

定义：二维前缀和是一种用于快速查询矩阵中任意子矩形区域元素之和的数据结构。它通过构建累积和矩阵，使得查询操作的时间复杂度降低到 $O(1)$。

构建方法：对于一个二维矩阵 $A$ 大小为 $m \times n$，定义二维前缀和矩阵 $Sum$ 使得：

$$Sum[i][j] = \sum_{x=1}^{i} \sum_{y=1}^{j} A[x][y],$$

即$Sum[i][j]$表示从矩阵左上角$(1, 1)$到位置$(i,j)$的子矩阵中所有元素的累加和。

递推公式：

$$Sum[i][j] = A[i][j] + Sum[i-1][j] + Sum[i][j-1] - Sum[i-1][j-1],$$

该公式中，减去 $Sum[i-1][j-1]$ 是为了消除重复累加的部分。

查询方法：要查询矩阵中任意子矩形区域$(x_1, y_1)$到$(x_2, y_2)$的和，可以通过以下公式快速得到：

$$\text{Result} = Sum[x_2][y_2] - Sum[x_1-1][y_2] - Sum[x_2][y_1-1] + Sum[x_1-1][y_1-1],$$

示例如下图所示，$[2,2]$到$[4,5]$矩形区域内的和$\text{Result} = Sum[4][5] - Sum[2][5] - Sum[4][2] + Sum[2][2]$，

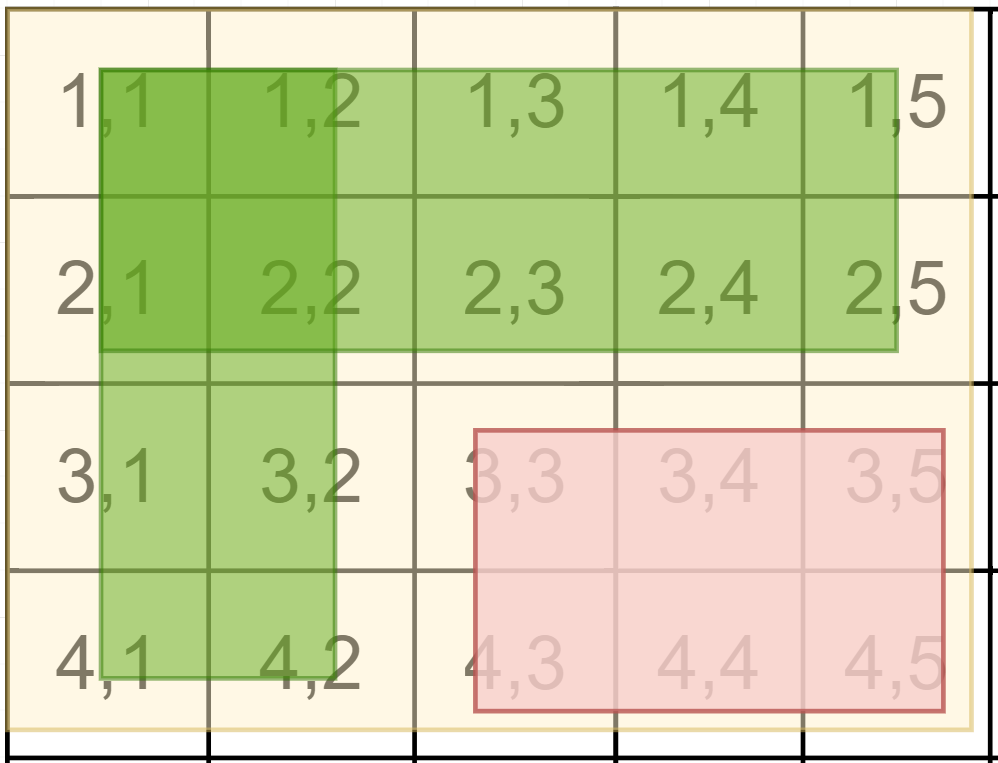
这里需要注意边界条件，即当$x_1$或$y_1$等于$1$时，减去的部分可能不存在。

代码实现：

# 假设我们有一个 m x n 的矩阵 A
A = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]

# 构建二维前缀和矩阵
m, n = len(A), len(A[0])
Sum = [[0] * (n + 1) for _ in range(m + 1)]

for i in range(1, m + 1):
    for j in range(1, n + 1):
        Sum[i][j] = A[i-1][j-1] + Sum[i-1][j] + Sum[i][j-1] - Sum[i-1][j-1]

# 查询子矩形 (2, 2) 到 (3, 3)
x1, y1, x2, y2 = 2, 2, 3, 3
result = Sum[x2][y2] - Sum[x1-1][y2] - Sum[x2][y1-1] + Sum[x1-1][y1-1]
print(f"查询区域和为: {result}")

复杂度分析：

• 预处理时间：$O(m \times n)$
• 查询时间：$O(1)$
• 空间复杂度：$O(m \times n)$

2. 二维差分

定义：二维差分扩展了一维差分的思想，适用于在二维矩阵中进行快速区间更新操作。通过构建差分矩阵 $D$，可以在 $O(1)$ 时间内更新矩阵的任意子矩形区域。

构建方法：对于给定的矩阵 $A$，定义二维差分矩阵 $D$ 为：

$$D[i][j] = A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1],$$

这个矩阵记录了位置$(i, j)$及其邻近位置的差异。

区间更新方法：为了在矩阵的子矩形区域$(x_1, y_1)$ 到$(x_2, y_2)$ 中增加一个值 $k$，需要在差分矩阵中进行以下操作：

• $D[x_1][y_1] += k$
• $D[x_1][y_2 + 1] -= k$（如果存在）
• $D[x_2 + 1][y_1] -= k$（如果存在）
• $D[x_2 + 1][y_2 + 1] += k$（如果存在）

更新后的矩阵恢复：构建完差分矩阵并进行更新后，通过对差分矩阵 $D$ 进行二维前缀和操作可还原出最终的矩阵 $A$。

代码实现：

# 初始化矩阵大小
m, n = 3, 3

# 初始化差分矩阵 D，大小为 (m+2) x (n+2)
D = [[0] * (n + 2) for _ in range(m + 2)]

# 执行一次区间更新，增加 k
def update(x1, y1, x2, y2, k):
    """
    对矩形区域 (x1, y1) 到 (x2, y2) 增加 k
    x1, y1, x2, y2 坐标基于 1 开始
    """
    D[x1][y1] += k
    if y2 + 1 <= n + 1:
        D[x1][y2 + 1] -= k
    if x2 + 1 <= m + 1:
        D[x2 + 1][y1] -= k
    if x2 + 1 <= m + 1 and y2 + 1 <= n + 1:
        D[x2 + 1][y2 + 1] += k

# 示例：执行几次区间更新
update(1, 1, 2, 2, 5)  # 矩形 (1, 1) 到 (2, 2) 增加 5
update(2, 2, 3, 3, 10) # 矩形 (2, 2) 到 (3, 3) 增加 10
update(1, 3, 3, 3, 3)  # 矩形 (1, 3) 到 (3, 3) 增加 3

# 对二维差分矩阵进行前缀和，得到最终的矩阵 D
for i in range(1, m + 1):
    for j in range(1, n + 1):
        D[i][j] += D[i-1][j] + D[i][j-1] - D[i-1][j-1]

# 恢复最终矩阵 A
A = [[0] * n for _ in range(m)]  # 初始化矩阵 A
for i in range(1, m + 1):
    for j in range(1, n + 1):
        A[i-1][j-1] = D[i][j]

# 输出结果
for row in A:
    print(row)

复杂度分析：

• 预处理时间：$O(1)$（只需初始化）
• 更新时间：单次更新为 $O(1)$
• 还原时间：二维前缀和计算的时间为 $O(m \times n)$
• 空间复杂度：$O(m \times n)$

3. 应用场景和总结

• 二维前缀和适用于快速查询任意子矩形的元素和，如图像处理、地图数据查询等。
• 二维差分非常适合对矩阵中进行多次批量区间更新，如对地图上多个区域施加增量操作或处理动态累计更新的问题。

通过扩展到二维，这两种算法继续发挥其高效处理区间问题的优势，为复杂的数据结构提供更好的解决方案。

例题：棋盘

小蓝拥有$n×n$大小的棋盘，一开始棋盘上全都是白子。

小蓝进行了$m$次操作，每次操作会将棋盘上某个范围内的所有棋子的颜色取反(也就是白色棋子变为黑色，黑色棋子变为白色)。

请输出所有操作做完后棋盘上每个棋子的颜色。

输入格式

输入的第一行包含两个整数$n,m$，用一个空格分隔，表示棋盘大小与操作数。

接下来$m$行每行包含四个整数$x_1,y_1,x_2,y_2$，相邻整数之间使用一个空格分隔，表示将在$x_1$至$x_2$行和$y_1$至$y_2$列中的棋子颜色取反。

输出格式

输出$n$行，每行$n$个$0$或$1$表示该位置棋子的颜色。

如果是白色则输出$0$，否则输出$1$。

数据范围

对于 $30\%$ 的评测用例，$1≤n,m≤500$；
对于所有评测用例，$1≤n,m≤2000, \le x_1 \le x_2 \le n, 1≤y_1≤y_2≤n$。

输入样例：

3 3
1 1 2 2
2 2 3 3
1 1 3 3

输出样例：

001
010
100

代码：

n, m = map(int, input().split())
maxN = 2010
diff = [[0] * maxN for _ in range(maxN)]

# 更新差分数组
for i in range(m):
    x1, y1, x2, y2 = map(int, input().split())
    diff[x1][y1] += 1
    diff[x2 + 1][y1] -= 1
    diff[x1][y2 + 1] -= 1
    diff[x2 + 1][y2 + 1] += 1

# 将差分数组进行前缀和，还原成原数组
for i in range(1, n + 1):
    for j in range(1, n + 1):
        diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1]
        # 判断当前颜色
        diff[i][j] %= 2

for i in range(1, n + 1):
    print(''.join(map(str, diff[i][1:n + 1])))